TỰ HỌC SAT MATH - SCATTER PLOT

Scatter plot hay Biểu đồ phân tán là một trong những dạng bài phổ biến nhất trong đề thi SAT nhưng lại không có trong các chương trình phổ thông tại Việt Nam (nếu bây giờ có rồi thì các mentor già của Moji xin lỗi) nên có thể khiến mọi người cảm thấy hơi lạ, dù thực chất thì cũng không có gì quá cao siêu.

I. Lý thuyết

1. Scatter Plot

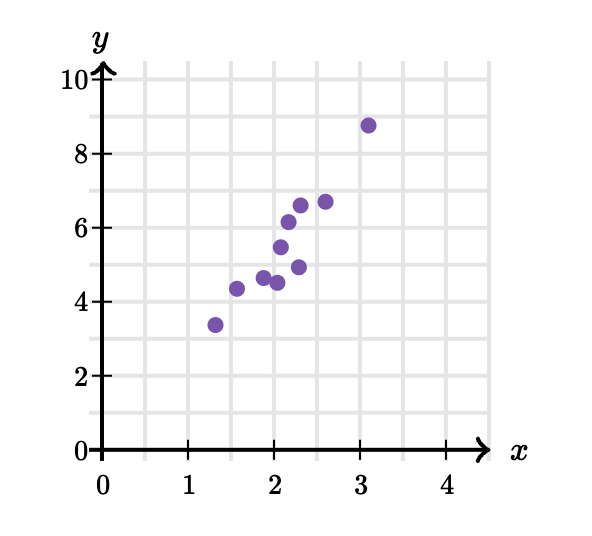
Scatter plot là một biểu đồ có trục x, y và mỗi điểm thể hiện một dữ liệu trong thế giới thật. Ví dụ

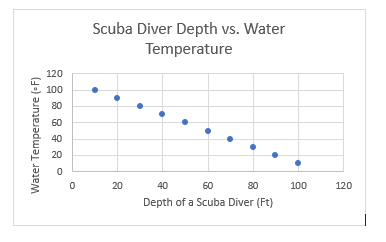
Biểu đồ trên có cột y là nhiệt độ nước, và trục x là độ sâu khi lặn dưới nước. Mình có thể đọc biểu đồ này theo cách: ở chấm trên cùng, với nhiệt độ nước là 100 độ F, thì mình đang ở độ sâu tầm 10 ft. Mình chỉ đơn giản là nhìn sang và xuống xem điểm mình đang để ý có giá trị x và y là gì, là đã làm được phần lớn các bài trong đề thi SAT rồi.

2. Line of best fit

Line of best fit sẽ là một được thẳng mà thể hiện xu hướng (trend) của dữ liệu. Mình có thể hiểu rằng các điểm dữ liệu sẽ là các giá trị thực còn đường thẳng sẽ là các giá trị được dự đoán. Thường sẽ chỉ là một đường thẳng được vẽ qua các điểm như hình dưới đây:

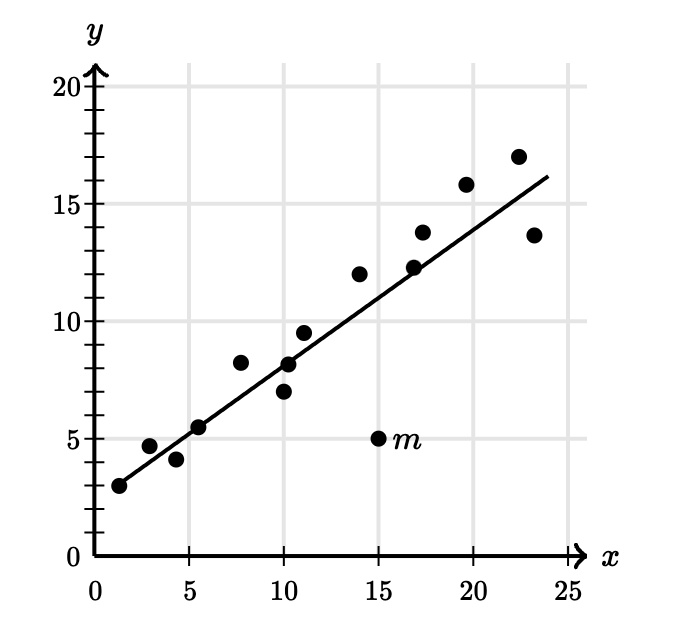
Như mình có thể thấy thì cái trend của những cái điểm dữ liệu (data points) là đi lên trên và cái đường đó thể hiện điều đấy. Một điều khác mình có thể nhận thấy là đường thẳng này không đi qua hết tất cả các điểm, và đây sẽ là một phần kiến thức quan trọng để làm các bài Line of best fit:

• Các điểm thuộc đường thẳng sẽ là những dự đoán chính xác nhất và thể hiện đúng xu hướng nhất
• Các điểm không thuộc đường thẳng sẽ có giá trị y khác so với đường thẳng, và cái khoảng cách giữa đường thẳng và điểm đó trên trục y chính là sự khác biệt giữa giá trị thực và giá trị được dự đoán tại một điểm x nào đó.

Những cái khác cần để ý sẽ là cái slope của đường thẳng, vì nó thể hiện xu hướng lên hoặc xuống, và rất hữu dụng trong những bài về xác định phương trình đường thẳng. Cái tiếp theo sẽ là chỗ mà đường thẳng cắt trục y, vì đó sẽ thể hiện giá trị của y khi mà x bằng 0 (sẽ rõ hơn ở phần dưới đây).

II. Các dạng thường thấy

1. Xác định sự khác biệt giữa giá trị thực và giá trị được dự đoán

Những bài này sẽ cho mình một biểu đồ, và hỏi rằng với giá trị x = 5 chẳng hạn thì giá trị thực của y khác với giá trị được dự đoán là bao nhiêu.

Giả sử với bài này, đề bài có thể hỏi là với x = 2000, giá nhà được dự đoán khác với giá nhà thật là bao nhiêu

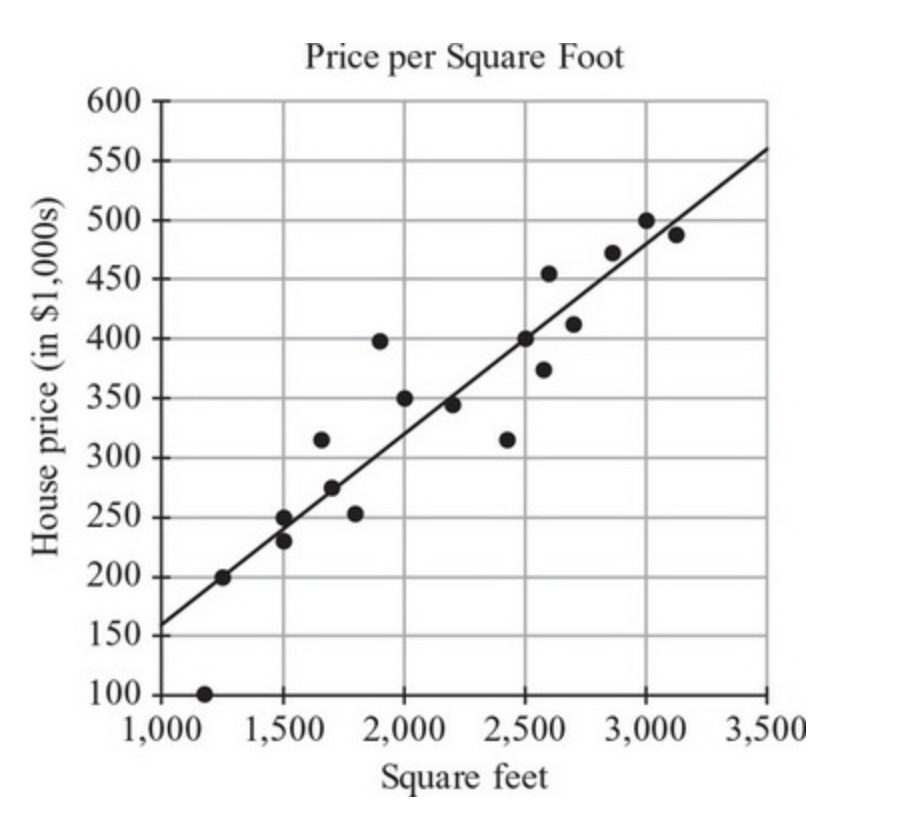
Thì ta có thể thấy là giá nhà thật tại x = 2000 là 350,000$ (tìm điểm x = 2000 rồi xem y bằng bao nhiêu) còn giá nhà được dự đoán sẽ cũng ở điểm 2000 nhưng mà lấy từ đường thẳng rồi nhìn qua thì y sẽ là tầm 320,000$ nên khác biệt sẽ là tầm 30,000$.

Một loại đề cũng khá gần bài này là xác định giá trị được dự đoán của y khi mà x không phải một giá trị thực. Họ có thể cho mình một phương trình của đường thẳng rồi hỏi mình với giá trị x bằng gì đó thì y bằng bao nhiêu. Trong trường hợp này thì chỉ đơn giản là thay x vào phương trình rồi tính ra giá trị y. Giả sử với phương trình y =5x + 20, thì đề bài có thể hỏi với giá trị x = 500 thì y bằng bao nhiêu (Chắc các bạn đều làm được nhỉ).

2. Xác định phương trình của Line of best fit dựa trên đồ thị

Bài này cũng đang trở nên ngày càng phổ biến và sẽ có 2 kiểu, một là line of best fit là đường thẳng, và 2 là line of best fit là một đường cong. Dù hình hài như thế nào thì cách làm vẫn sẽ như thế thôi, đó là mình dựa vào slope và các điểm trên đồ thị. Khi đồ thị là một đường thẳng thì có phương trình là y = ax + b thì slope sẽ là a

Bước 1: Xác định slope âm hoặc dương. Đồ thị có thể hướng lên trên / hoặc xuống dưới \. Lên trên thì sẽ là slope dương và xuống dưới sẽ là slope âm. Điều này đã đủ để khiến mình loại 2 trong 4 đáp án rồi, vì các đáp án thường sẽ là 2 đáp án khác nhau nhưng mỗi đáp án có 2 phiên bản là slope âm hoặc dương. Điều này cũng tương tự với các đường cong, cong lên là dương và xuống là âm.

Mình có thể thấy là cũng chỉ có 2 đáp án nhưng mỗi đáp án có 2 phiên bản, và trong bài này (chưa cần để ý hình vội) thì cứ biết là đồ thị cong lên nên "slope" (với đồ thị parabol thì nó sẽ là mở lên trên hoặc mở xuống dưới nhưng mình dùng slope để dễ hình dung) sẽ dương và là đáp án A hoặc C.

Bước 2: Dựa vào điểm cắt trục y của đồ thị, thường với các bài này thì điểm cắt trục y sẽ là cái thể hiện điểm khác biệt lớn giữa 2 đáp án, và lý do mình sử dụng điểm này là vì nó rất dễ tìm, đơn giản là mình thay x = 0 thôi. Thì với ví dụ ở trên mình sẽ có y = 969 hoặc 0.969, khác biệt vô cùng lớn.

Và dựa vào đồ thị này thì ta có thể thấy là khi mà x = 0 thì y cũng bằng 0 hay rất sát với 0 nhưng mà chắc chắn không thể là 969 được, nên có thể nhanh chóng chọn đáp án A.

Với đường thẳng cách làm cũng sẽ không khác gì, loại đáp án -> tìm điểm giao với trục y. Trong trường hợp vô cùng hiếm có khó tìm mà điểm giao với trục y của các đáp án trùng nhau, thì mình hãy thay các điểm trên đường thẳng vào phương trình, chỉ cần thay 3 điểm thoả mãn thôi là đảm bảo tìm được đáp án đúng.

3. Xác định ý nghĩa của các giá trị trên đồ thị

Dạng 1: Xác định ý nghĩa của giao điểm với trục y
Như mình đã biết thì giao điểm với trục y là khi mà x = 0. Vậy thì mình có thể nhanh chóng kết luận là giao điểm y là giá trị của đơn vị được thể hiện bởi trục y khi mà đơn vị được thể hiện bởi trục x  là 0.

Ở bài dưới đây thì trục y là số điểm, trục x là "thời gian còn thừa khi học sinh nộp bài", và giao điểm với trục y là 87 (Đề bài cho)

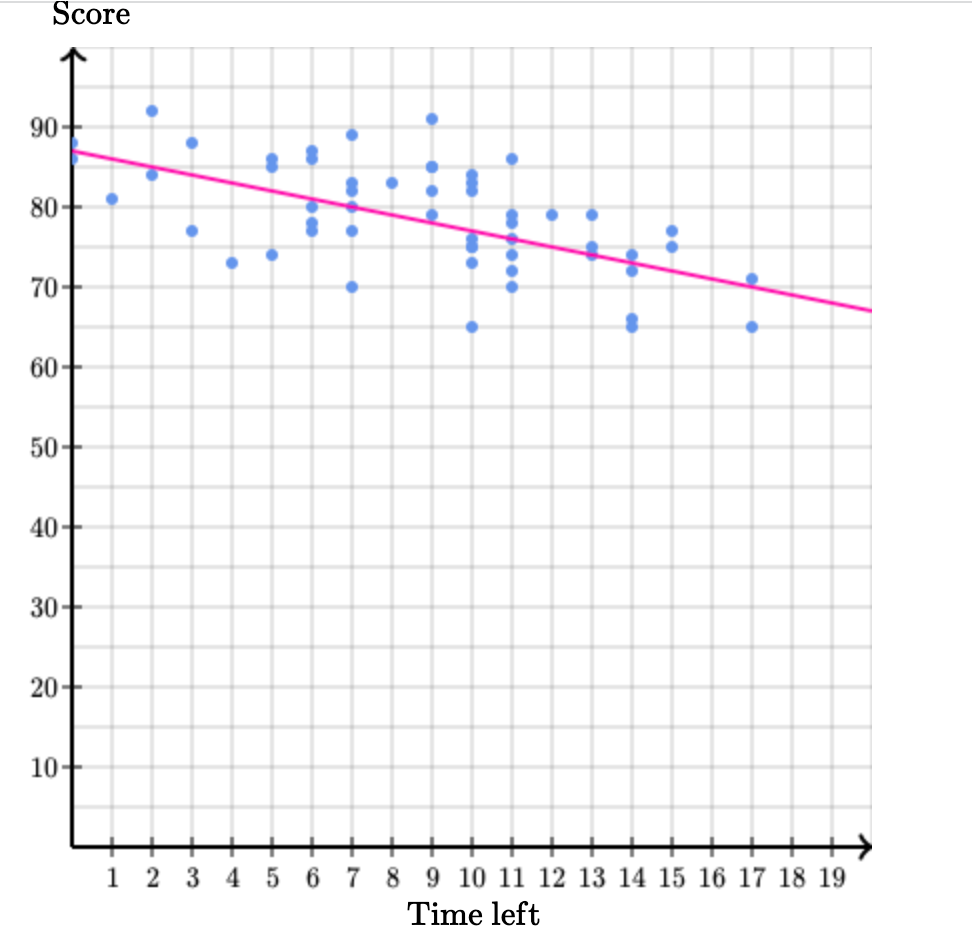
Với thông tin trên, mình biết là với y = 87 thì x = 0, x là thời gian còn lại và y là số điểm, vậy nên ý nghĩa là khi mà học sinh nộp bài khi còn 0 phút (hay đúng vào lúc hết giờ) thường có số điểm là 87. Đáp án đúng là:

Dạng 2: Xác định ý nghĩa của slope

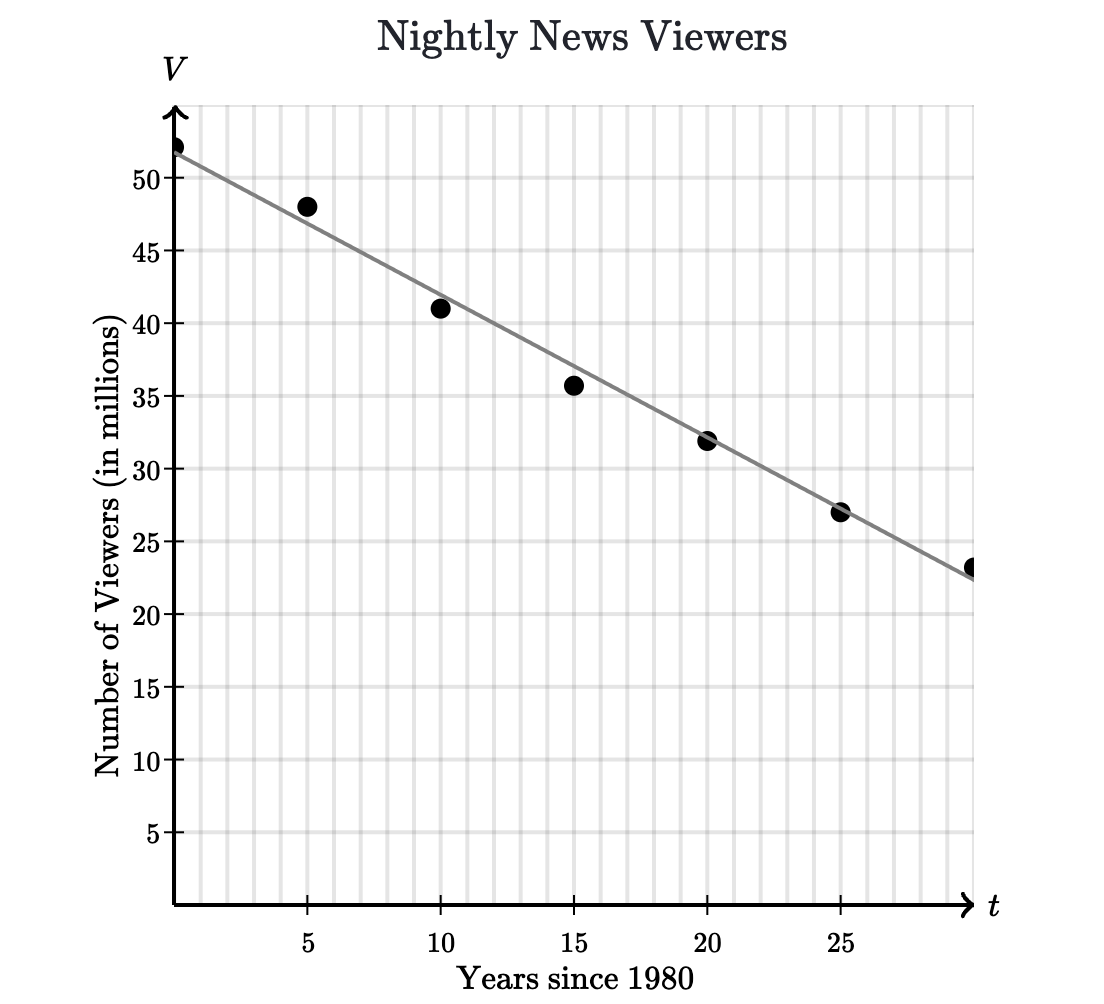
Slope là mức độ thay đổi của đồ thị theo từng đơn vị của trục x. Mình có thể hiểu đơn giản là như thế này:
y = 5x + b
Ta có, slope là 5, vậy thì khi mà x tăng 1 đơn vị thì y tăng 5 đơn vị, tức là slope là mức thay đổi của y mỗi khi x tăng hoặc giảm 1 đơn vị. Vậy thì trong bài này, đơn vị của x là số năm, vậy đáp án phải là mức độ thay đổi theo số năm.

Bước tiếp theo là mình cần nhìn xem vậy thì khi x thay đổi như thế thì y thay đổi như thế nào. Mình có thể nhìn đơn giản trên hình là khi x = 5 thì y =47 và khi x = 6 thì y = 46. Điều này tức là cứ qua một năm thì y giảm 1 triệu, và đó cũng là đáp án.

Bài học hôm nay đến đây là kết thúc, các bạn có câu hỏi gì thì hãy hỏi trên TikTok của chúng mình tại @odayco1600sat và chúc mọi người ôn tập SAT thành công nhé 💯💯💯.