TỰ HỌC SAT MATH - LINEAR FUNCTIONS

Linear functions hay hàm số tuyến tính là dạng cực kì, cực kì quan trọng trong SAT, lý thuyết thì đơn giản và quen thuộc với các học sinh Việt, nhưng dạng bài thì vô cùng đa dạng.

Một hàm tuyến tính là một hàm tạo thành một đường thẳng trong một đồ thị, và là một hàm đa thức mà bậc của nó lớn nhất là 1 hoặc 0. Đồ thị hàm tuyến tính có một đường thẳng với công thức như sau.

y = f (x) = ax + b

Khái niệm

• x trong f(x) được gọi là independent variable (Nhưng với SAT chỉ cần biết tới là variable hay "biến")
• y trong y = f(x) được gọi là dependent variable
• Hướng/Slope: thường ký hiệu là a trong y = ax + b thể hiện hướng của đường thẳng. a dương thì slope dương và đường thẳng đi lên, âm thì xuống dưới
• y-intercept: thường ký hiệu là b, đây là giá trị của hàm số khi x = 0

Với SAT thì mình sẽ chia Hàm tuyến tính (Linear functions) và Phương trình tuyến tính (Linear equations) là hai dạng khác nhau để mọi người dễ học. Linear functions thì sẽ là các bài liên quan tới đồ thị hàm số, còn Linear equations là những bài về phương trình bậc 1 còn lại.

Phần lý thuyết này thì mọi người cũng gặp khá nhiều nên cũng khá quen thuộc rồi, bây giờ mình sẽ đi đến các dạng bài phổ biến từ dễ đến khó nha.

Loại 1: Áp dụng kiến thức cơ bản về đồ thị

Dạng này thường sẽ hỏi mình áp dụng lý thuyết, ý nghĩa của x, y, slope, hoặc y-intercept.

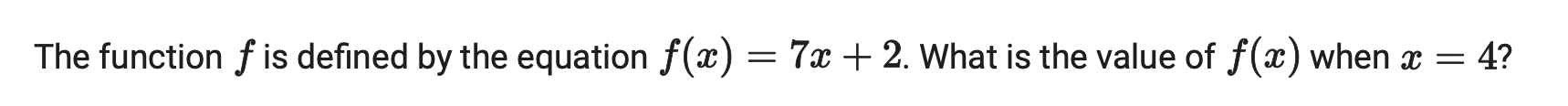
Mình có thể thấy là cả 3 câu này đều khá đơn giản, và mình có thể dễ dàng làm được nếu mà hiểu khái niệm cơ bản liên quan tới đồ thị hàm số.

Loại 2: Biểu diễn đồ thị hàm số theo cách khác

Mình hay quen với việc thể hiện đồ thị hàm số qua phương trình hay đồ thị, thì ở các dạng này SAT có thể thể hiện qua toán có lời văn, hoặc qua bảng.

Dạng toán có lời văn thì sẽ giao với dạng Interpretation, và mình sẽ cần hiểu xem mỗi giá trị được nhắc tới thật ra là gì. Như trong ví dụ trên thì f(x) là giá trị được dự đoán, a ở trên là y-intercept, b là slope (mức độ thay đổi), còn x là số ngày sau khi ra đời. Mình biết là khi mới ra đời hay x = 0 thì con đó nặng 241 pounds, thay vào phương trình thì ta có 241 = a + 0b = a. Vậy nên mình tìm được a là 241.

Mình có thể thấy là cách làm sẽ chỉ là xác định ý nghĩa xong thay vào phương trình.

Với ví dụ này, mình sẽ dựa vào bảng có 2 giá trị là x và giá trị tương ứng của hàm số với mỗi giá trị của x. Bài này cách tiếp cận cũng sẽ là thay số vào cho đến khi mình tìm được đáp án phù hợp. Với x = 1 thì f(x) = -64, tức là -64 = a + b. Sau đó mình có với x = 2 thì f(x) = 0. Vậy nên 0 = 2a + b. Chỉ từ 2 cái trên là mình đã ra được một hệ phương trình

-64 = a + b
0 = 2a + b

Và mình có thể giải được 2a + b - a - b = 64, vậy nên a = 64 và b = - 128. Vậy a - b = 192

Loại 3: Các dạng liên quan tới đồ thị

Các dạng này sẽ yêu cầu mình xác định và áp dụng các kiến thức trên nhưng sẽ qua một đồ thị. Đề bài có thể hỏi mình tìm đồ thị dựa trên phương trình được cho, hoặc giải một bài toán có lời văn dựa trên đồ thị được cho.

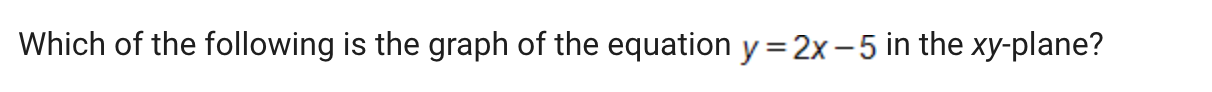
Mình có thể để ý ngay là slope = 2 nên đường thẳng hướng lên trên, và y-intercept tại -5. Nên nhanh chóng thấy được luôn đáp án là đây

Các bài mà có đồ thị thường sẽ khá là dễ làm, vì rất dễ sử dụng phương pháp loại trừ chỉ qua việc nhìn lướt.

Bài học hôm nay đến đây là kết thúc, các bạn có câu hỏi gì thì hãy hỏi trên TikTok của chúng mình tại @odayco1600sat và chúc mọi người ôn tập SAT thành công nhé 💯💯💯.