TỰ HỌC SAT MATH - CIRCLE EQUATION

Bài học hôm nay Moji muốn gửi tới mọi người là Phương trình đường tròn, hay Circle equation. Với các bạn năm nay học lớp 12 thì phần này sẽ quá là đơn giản, nhưng với các bạn thi SAT năm lớp 10 hay 11 thì sẽ hơi gặp khó khăn bỡ ngỡ một chút.

I. Lý thuyết

Trên mặt phẳng xy, một đường tròn với tâm (h, k) và bán kính r sẽ có phương trình là:

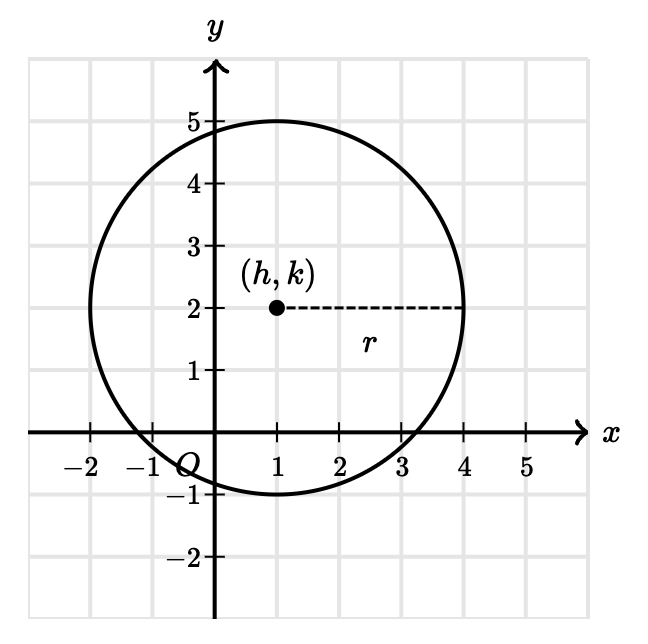
Điều này là bởi vì phương trình đó thể hiện tất cả những điểm mà cách tâm (h, k) một khoảng r. Tức là khi mà mình thay điểm (x, y) vào phương trình và thoả mãn thì điểm đó nằm trên đường tròn.

Mình ra được phương trình này từ công thức tính khoảng cách giữa 2 điểm. Khoảng cách giữa tâm (h, k) và một điểm bất kì (x, y) trên đường tròn sẽ là:

Khoảng cách này sẽ bằng bán kính r, nên ta sẽ ra được phương trình

Khi ta bình phương để mất dấu căn ta sẽ được

Ví dụ:

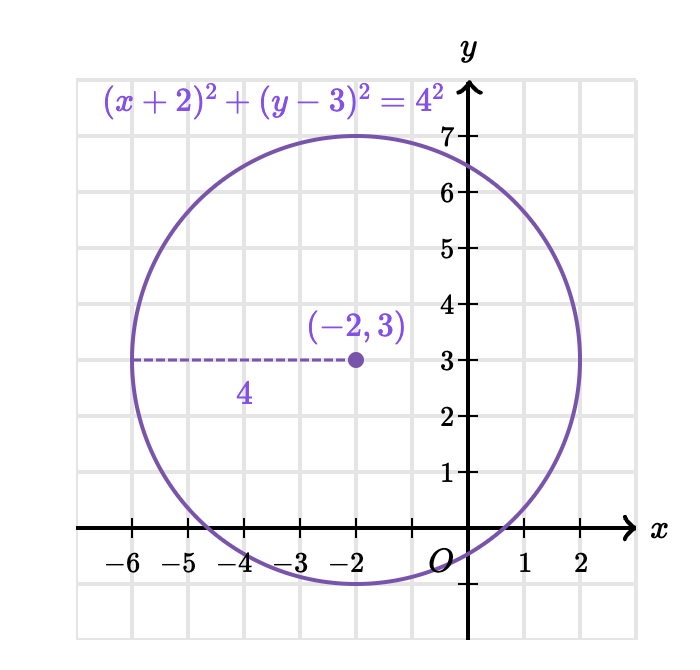
Với phương trình dưới đây thì ta có x = -2 và y = 3 sẽ là tâm của hình tròn và r =4 là bán kính

II. Những dạng bài hay được hỏi trong đề SAT

1. Áp dụng phương trình đường tròn

Dạng bài này thường khá là đa dạng, nhưng đều sẽ quy về xác định phương trình, tâm, hoặc bán kính của đường tròn. Thường thì mình sẽ phải làm phép biến đổi để đưa phương trình về dạng cơ bản trước khi làm bài.

Khi mà đề bài cho mình phương trình

Mình cần phải đưa nó về dạng

Thì việc đầu tiên sẽ phải là tìm dạng x và y ở trong ngoặc. Ở đây ta để ý thấy +2x và -10y. Vậy thì qua hằng đẳng thức bậc 2 ta có thể thêm bớt vào sau để có thể đạt được dạng mong muốn.

Mình thấy là mình có +22 nên có thể biến đổi thành 1 + 25 - 4 để thoả mãn hằng đẳng thức

Ta thấy 4 có thể chuyển sang vế phải và biến thành 2 bình phương và ta đã có một phương trình đúng với dạng cơ bản.

Để làm dạng này thì miễn là mình nắm chắc đâu là tâm, đâu là bán kính trong phương trình đường tròn thì bài nào cũng làm được.

2. Dịch chuyển đường tròn

Đây là dạng bài mà mình cảm thấy là được hỏi khá thường xuyên trong đề thi SAT và nó áp dụng một chút kiến thức của phần dịch chuyển đồ thị mà mình đã giải thích kỹ hơn ở bài này. Tuy nhiên, phương trình đường tròn lại không giống những phương trình khác khi mà mọi loại dịch chuyển đều khá giống với cảm tính.
Những bài dạng này sẽ yêu cầu mình tìm tâm hoặc phương trình mới của đường tròn sau khi bị dịch chuyển lên, xuống, sang trái, hoặc sang phải.

Phương trình gốc

Dịch đồ thị sang phải (cộng thêm vào h):

Dịch đồ thị sang trái (trừ vào h):

Dịch đồ thị lên (cộng vào k):

Dịch đồ thị xuống (trừ vào k):

Kết hợp (hiếm gặp):

Lý do mà các phép dịch chuyển ngược lại cũng khá phức tạp, nhưng có thể hiểu đơn giản là trên kia mình đang không thay đổi x như các bài trước mà mình đang thay đổi tâm (h, k).

Ngoài ra thì bài có thể hỏi về tăng bán kính nhưng phần này thì khá đơn giản. Giả sử nếu tăng bán kính lên gấp 3 lần ban đầu, thì bán kính từ

Hoặc là tăng thêm 5 đơn vị:

và phần còn lại của phương trình thì cứ giữ nguyên không cần thay đổi.

Và

III. Đề thi từ College Board

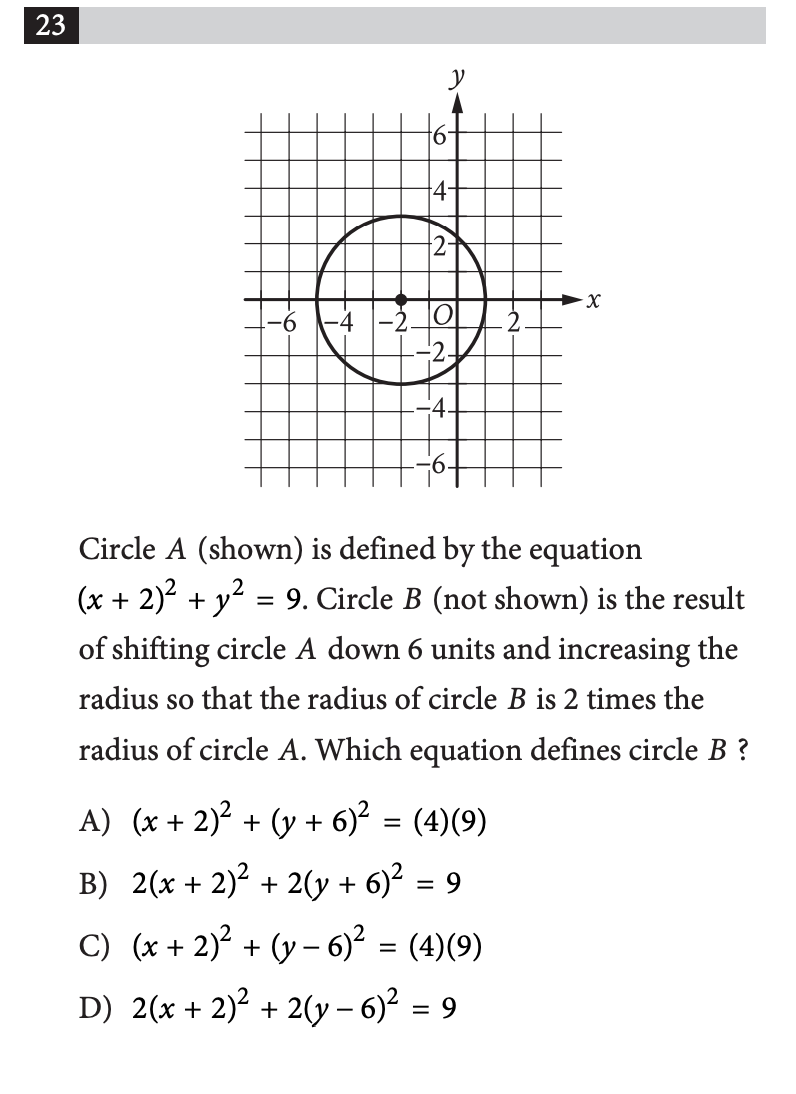
Đề bài yêu cầu ta tìm phương trình của đường tròn B, là kết quả của việc dịch đường tròn A xuống 6 đơn vị và tăng gấp đôi bán kính của đường tròn A. Bài này yêu cầu ta vận dụng khá nhiều phần kiến thức đã học ở trên, và để giải được thì bước đầu tiên sẽ là dịch chuyển đồ thị.

Để dịch chuyển đường tròn A xuống 6 đơn vị thì ta cần trừ vào k trong tâm (h, k) của đường tròn. Phương trình dịch chuyển xuống:

Thay số vào phương trình trên:

Vì tâm là (-2, 0) nên trong phương trình thì (y - 0). Và qua hình ta có thể thấy được bán kính r = 3. Vậy nên khi dịch chuyển xuống thì mình thay b trong phương trình gốc bằng 6, để giảm toạ độ của tâm (h, k) thành (-2, -6).

Sau đó, ta phải tăng bán kính lên gấp 2 lần. Thì ta chỉ cần thay trực tiếp vào bán kính hiện tại là r = 3 thì sẽ thành r =3.2 và

Ta có phương trình cuối cùng là:

Vậy đáp án đúng sẽ là đáp án A.

Bài học hôm nay đến đây là kết thúc, các bạn có câu hỏi gì thì hãy hỏi trên TikTok của chúng mình tại @odayco1600sat và chúc mọi người ôn tập SAT thành công nhé 💯💯💯.